9.12. Building the Knight’s Tour Graph¶
To represent the knight’s tour problem as a graph we will use the following two ideas: Each square on the chessboard can be represented as a node in the graph. Each legal move by the knight can be represented as an edge in the graph. Figure 1 illustrates the legal moves by a knight and the corresponding edges in a graph.
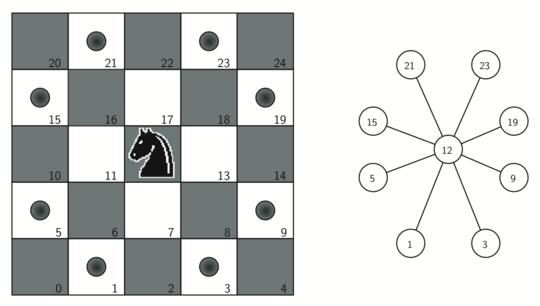
Figure 1: Legal Moves for a Knight on Square 12, and the Corresponding Graph
To build the full graph for an n-by-n board we can use the C++
function shown in Listing 1. The knightGraph function
makes one pass over the entire board. At each square on the board the
knightGraph function calls a helper, genLegalMoves, to create a
list of legal moves for that position on the board. All legal moves are
then converted into edges in the graph. Another helper function
coordToNum converts a location on the board in terms of a row and a
column into a linear vertex number similar to the vertex numbers shown
in Figure 1.
Listing 1
Graph knightGraph(int bdSize) {
Graph ktGraph(false);
for (int row = 0; row < bdSize; row++) {
for (int col = 0; col < bdSize; col++) {
int nodeId = coordToNum(row, col, bdSize);
vector<int> newPositions = genLegalMoves(nodeId, bdSize);
for (int i = 0; i < newPositions.size(); i++) {
int newId = newPositions[i];
ktGraph.addEdge(nodeId, newId);
}
}
}
return ktGraph;
}
The genLegalMoves function (Listing 2) takes the position of the knight on the
board and generates each of the eight possible moves. The legalCoord
helper function (Listing 2) makes sure that a particular move that is generated is
still on the board.
Listing 2
int coordToNum(int x, int y, int bdSize) {
// Takes the x y position and returns the id from 0 to (bdSize*2)-1
int id = 0;
id += y * bdSize;
id += x;
return id;
}
pair<int, int> numToCoord(int id, int bdSize) {
int x, y;
x = id % bdSize;
y = (id - x) / bdSize;
return make_pair(x, y);
}
bool legalCoord(int x, int bdSize) {
if (x >= 0 && x < bdSize) {
return true;
} else {
return false;
}
}
vector<int> genLegalMoves(int id, int bdSize) {
pair<int, int> coords = numToCoord(id, bdSize);
int x = coords.first;
int y = coords.second;
vector<int> newMoves;
vector<pair<int, int>> myVec = {
{-1, -2}, {-1, 2}, {-2, -1}, {-2, 1}, {1, -2}, {1, 2}, {2, -1}, {2, 1}};
for (unsigned int i = 0; i < myVec.size(); i++) {
int newX = x + myVec[i].first;
int newY = y + myVec[i].second;
if (legalCoord(newX, bdSize) && legalCoord(newY, bdSize)) {
newMoves.push_back(coordToNum(newX, newY, bdSize));
}
}
return newMoves;
}
Figure 2 shows the complete graph of possible moves on an eight-by-eight board. There are exactly 336 edges in the graph. Notice that the vertices corresponding to the edges of the board have fewer connections (legal moves) than the vertices in the middle of the board. Once again we can see how sparse the graph is. If the graph was fully connected there would be 4,096 edges. Since there are only 336 edges, the adjacency matrix would be only 8.2 percent full.

Figure 2: All Legal Moves for a Knight on an \(8 \times 8\) Chessboard
The full implementation of this is shown below, however the code must be ran in C++11
due to differences in Vector Initialization between C++ versions. In the below code,
in the main function, we traverse using our previously created breadth-first search between
two locations. In the next chapter, we will implement a different algorithm called a
depth first search (DFS) to solve our knight’s tour problem.
#include <fstream>
#include <iostream>
#include <map>
#include <queue>
#include <string>
#include <vector>
using namespace std;
class Vertex {
public:
int id;
map<int, float> connectedTo;
// Added for Breadth-First Algorithm
char color;
float dist;
Vertex *pred;
Vertex() {
// w for white, g for grey, b for black
color = 'w';
dist = 0;
pred = NULL;
}
Vertex(int key) {
id = key;
color = 'w';
dist = 0;
pred = NULL;
}
void addNeighbor(int nbr, float weight = 1) {
connectedTo[nbr] = weight;
}
vector<int> getConnections() {
vector<int> keys;
// Use of iterator to find all keys
for (map<int, float>::iterator it = connectedTo.begin();
it != connectedTo.end();
++it) {
keys.push_back(it->first);
}
return keys;
}
int getId() {
return id;
}
float getWeight(int nbr) {
return connectedTo[nbr];
}
friend ostream &operator<<(ostream &, Vertex &);
};
ostream &operator<<(ostream &stream, Vertex &vert) {
vector<int> connects = vert.getConnections();
stream << vert.id << " -> ";
for (unsigned int i = 0; i < connects.size(); i++) {
stream << connects[i] << endl << "\t";
}
return stream;
}
class Graph {
public:
map<int, Vertex> vertList;
int numVertices;
bool directional;
Graph(bool directed = true) {
directional = directed;
numVertices = 0;
}
Vertex addVertex(int key) {
numVertices++;
Vertex newVertex = Vertex(key);
this->vertList[key] = newVertex;
return newVertex;
}
Vertex *getVertex(int n) {
return &vertList[n];
}
bool contains(int n) {
for (map<int, Vertex>::iterator it = vertList.begin();
it != vertList.end();
++it) {
if (it->first == n) {
return true;
}
}
return false;
}
void addEdge(int f, int t, float cost = 1) {
if (!this->contains(f)) {
this->addVertex(f);
}
if (!this->contains(t)) {
this->addVertex(t);
}
vertList[f].addNeighbor(t, cost);
if (!directional) {
vertList[t].addNeighbor(f, cost);
}
}
vector<int> getVertices() {
vector<int> verts;
for (map<int, Vertex>::iterator it = vertList.begin();
it != vertList.end();
++it) {
verts.push_back(it->first);
}
return verts;
}
friend ostream &operator<<(ostream &, Graph &);
};
ostream &operator<<(ostream &stream, Graph &grph) {
for (map<int, Vertex>::iterator it = grph.vertList.begin();
it != grph.vertList.end();
++it) {
stream << grph.vertList[it->first];
cout << endl;
}
return stream;
}
Graph bfs(Graph g, Vertex *start) {
start->dist = 0;
start->pred = NULL;
queue<Vertex *> vertQueue;
vertQueue.push(start);
while (vertQueue.size() > 0) {
Vertex *currentVert = vertQueue.front();
vertQueue.pop();
for (unsigned int nbr = 0; nbr < currentVert->getConnections().size();
nbr++) {
if (g.vertList[currentVert->getConnections()[nbr]].color == 'w') {
g.vertList[currentVert->getConnections()[nbr]].color = 'g';
g.vertList[currentVert->getConnections()[nbr]].dist =
currentVert->dist + 1;
g.vertList[currentVert->getConnections()[nbr]].pred =
currentVert;
vertQueue.push(&g.vertList[currentVert->getConnections()[nbr]]);
}
}
currentVert->color = 'b';
}
return g;
}
void traverse(Vertex *y) {
Vertex *x = y;
int count = 1;
while (x->pred) {
cout << x->id << " to " << x->pred->id << endl;
x = x->pred;
count++;
}
}
int coordToNum(int x, int y, int bdSize) {
// Takes the x y position and returns the id from 0 to (bdSize*2)-1
int id = 0;
id += y * bdSize;
id += x;
return id;
}
pair<int, int> numToCoord(int id, int bdSize) {
int x, y;
x = id % bdSize;
y = (id - x) / bdSize;
return make_pair(x, y);
}
bool legalCoord(int x, int bdSize) {
if (x >= 0 && x < bdSize) {
return true;
} else {
return false;
}
}
vector<int> genLegalMoves(int id, int bdSize) {
pair<int, int> coords = numToCoord(id, bdSize);
int x = coords.first;
int y = coords.second;
vector<int> newMoves;
vector<pair<int, int>> myVec = {
{-1, -2}, {-1, 2}, {-2, -1}, {-2, 1}, {1, -2}, {1, 2}, {2, -1}, {2, 1}};
for (unsigned int i = 0; i < myVec.size(); i++) {
int newX = x + myVec[i].first;
int newY = y + myVec[i].second;
if (legalCoord(newX, bdSize) && legalCoord(newY, bdSize)) {
newMoves.push_back(coordToNum(newX, newY, bdSize));
}
}
return newMoves;
}
Graph knightGraph(int bdSize) {
Graph ktGraph(false);
for (int row = 0; row < bdSize; row++) {
for (int col = 0; col < bdSize; col++) {
int nodeId = coordToNum(row, col, bdSize);
vector<int> newPositions = genLegalMoves(nodeId, bdSize);
for (int i = 0; i < newPositions.size(); i++) {
int newId = newPositions[i];
ktGraph.addEdge(nodeId, newId);
}
}
}
return ktGraph;
}
int main() {
Graph kt = knightGraph(8);
kt = bfs(kt, kt.getVertex(63));
traverse(kt.getVertex(0));
return 0;
}