2.2. What Is Algorithm Analysis?¶
It is very common for beginning computer science students to compare their programs with one another. You may also have noticed that it is common for computer programs to look very similar, especially the simple ones. An interesting question often arises. When two programs solve the same problem but look different, is one program better than the other?
In order to answer this question, we need to remember that there is an important difference between a program and the underlying algorithm that the program is representing. As we stated in Chapter 1, an algorithm is a generic, step-by-step list of instructions for solving a problem. It is a method for solving any instance of the problem such that given a particular input, the algorithm produces the desired result. A program, on the other hand, is an algorithm that has been encoded into some programming language. There may be many programs for the same algorithm, depending on the programmer and the programming language being used.
To explore this difference further, consider the function shown in ActiveCode 1. This function solves a familiar problem, computing the sum of the first n integers. The algorithm uses the idea of an accumulator variable that is initialized to 0. The solution then iterates through the n integers, adding each to the accumulator.
Listing 1
Now look at the function in ActiveCode 2. At first glance it may look strange, but upon further inspection you can see that this function is essentially doing the same thing as the previous one. The reason this is not obvious is poor coding. We did not use good identifier names to assist with readability, and we used an extra assignment statement during the accumulation step that was not really necessary.
Listing 2
The question we raised earlier asked whether one function is better than
another. The answer depends on your criteria. The function sumOfN is
certainly better than the function foo if you are concerned with
readability. In fact, you have probably seen many examples of this in
your introductory programming course since one of the goals there is to
help you write programs that are easy to read and easy to understand. In
this course, however, we are also interested in characterizing the
algorithm itself. (We certainly hope that you will continue to strive to
write readable, understandable code.)
Algorithm analysis is concerned with comparing algorithms based upon the amount of computing resources that each algorithm uses. We want to be able to consider two algorithms and say that one is better than the other because it is more efficient in its use of those resources or perhaps because it simply uses fewer. From this perspective, the two functions above seem very similar. They both use essentially the same algorithm to solve the summation problem.
At this point, it is important to think more about what we really mean by computing resources. There are two different ways to look at this. One way is to consider the amount of space or memory an algorithm requires to solve the problem. The amount of space required by a problem solution is typically dictated by the problem instance itself. Every so often, however, there are algorithms that have very specific space requirements, and in those cases we will be very careful to explain the variations.
As an alternative to space requirements, we can analyze and compare
algorithms based on the amount of time they require to execute. This
measure is sometimes referred to as the “execution time” or “running
time” of the algorithm. One way we can measure the execution time for
the function sumOfN is to do a benchmark analysis. This means that
we will track the actual time required for the program to compute its
result. In C++, we can benchmark a function by noting the starting
time and ending time with respect to the system we are using. In the
ctime library there is a function called clock that will return the
current system clock time in seconds since some arbitrary starting
point. By calling this function twice, at the beginning and at the end,
and then computing the difference, we can get an exact number of seconds
(fractions in most cases) for execution.
Listing 3
Listing 3 shows the original sumOfN function with the timing
calls embedded before and after the summation. The function returns the amount of time (in seconds)
required for the calculation.
Consider the following code block:
int n = 1000;
int theSum = 0;
for (int i=0; i<n+1; i++){
theSum = theSum + 1; //how many times?
}
Q-1: How many times is the count = count + 1 line executed?
2.2.1. Some Needed Math Notation¶
This is the sigma symbol: \(\sum_{}\). It tells us that we are summing up something much like a mathematical loop typically with a counter.
If we have \(\sum_{i=1}^{5}\) the bottom index i=1 tells us that the index i begins at 1 and that i will terminate at 5.
What ever comes immediately afterwards is what we are summing. So, \(\sum_{i=1}^{5} i\) tells us to add the integers \(1+2+3+4+5\) because just like in a for loop, we plug a value for each i value. Similarly, \(\sum_{i=2}^{4} i^2\) means \(2^2+3^2+4^2\).
-
Q-2: Compute the result of \(\sum_{i=1}^{3} i^3\)
- 6
- No. Use i = 1, i = 2, and i = 3, plugging into i^3.
- 14
- No. Use i = 1, i = 2, and i = 3, plugging into i^3.
- 25
- No. Use i = 1, i = 2, and i = 3, plugging into i^3.
- 36
- Right! It is 1^3 + 2^3 + 3^3 = 1 + 8 + 27.
- None of the above.
- One of the above is correct!
2.2.2. Applying the Math Notation¶
There is often more than one way to solve a problem. Let’s consider the blue area in the following \(8 \times 9\).rectangle.
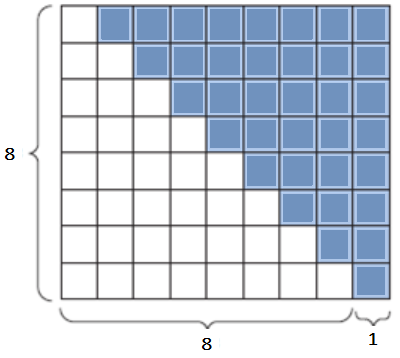
Figure 1: Sum of n = 8 integers
To find the blue area, we can count the number of blue squares \(1+2+3+4+5+6+7+8\), which we just learned can be written as \(\sum_{i=1}^{8} i.\) However, we also know how to find the area of a rectangle, by multiplying height by width, and the blue squares represent half of the rectangle. So, the area with blue squares is also just \(\sum_{i=1}^{8} i = \frac {(8)(8+1)}{2}\).
Hence, when we have a variable n, we have learned that we can just the
closed equation \(\sum_{i=1}^{n} i = \frac {(n)(n+1)}{2}\) to
compute the sum of the first n integers without iterating.
Consider the following function:
int sumOfN3(int n){
int sum_n = (n*(n+1))/2; // how many times?
return sum_n;
}
Q-3: If SumOfN3 is called once with a parameter of n=10, how many times is the int sum_n = (n*(n+1))/2; line executed?
We see this in ActiveCode 4,
which shows sumOfN3
taking advantage of the formula we just developed.
If we do the same benchmark measurement for sumOfN3,
using the value 10,000 for n and we get the following result:
Sum is 50005000 required 0.000000 seconds
Sum is 50005000 required 0.000000 seconds
Sum is 50005000 required 0.000001 seconds
Sum is 50005000 required 0.000001 seconds
Sum is 50005000 required 0.000000 seconds
There are two important things to notice about this output. First, the
times recorded above are shorter than any of the previous examples.
Second, they are very consistent no matter what the value of n. It
appears that sumOfN3 is hardly impacted by the number of integers
being added.
But what does this benchmark really tell us? Intuitively, we can see
that the iterative solutions seem to be doing more work since some
program steps are being repeated. This is likely the reason it is taking
longer. Also, the time required for the iterative solution seems to
increase as we increase the value of n. However, there is a problem.
If we ran the same function on a different computer or used a different
programming language, we would likely get different results. It could
take even longer to perform sumOfN3 if the computer were older.
We need a better way to characterize these algorithms with respect to execution time. The benchmark technique computes the actual time to execute. It does not really provide us with a useful measurement, because it is dependent on a particular machine, program, time of day, compiler, and programming language. Instead, we would like to have a characterization that is independent of the program or computer being used. This measure would then be useful for judging the algorithm alone and could be used to compare algorithms across implementations.